The golden ratio is the name of the harmony between the parts or stages that constitute a whole, which can be seen in our daily life, in nature or in the universe, any time or place.
What is the Golden Ratio?
The Golden Ratio, which we can call the most beautiful harmony of the parts that make up a whole as we mentioned before, is the string of numbers starting with 1.61803389. The symbol of the Golden Ratio is Phi,Φ.
For example, if we divide the black line into two parts according to the Golden Ratio, the ratio of red part to the blue and the ratio of the blue part to the black is equal.

The Fibonacci string or Fibonacci numbers emerged after Leonardo of Pisa asked the following problem in his book Liber Abaci, in which he described the Indian-Arab numbers. You can learn more about Leonardo Fibonacci from this page.
The problem asks this question,
Put a pair of rabbits in a room with all sides surrounded by walls. How many pairs of rabbits are there at the end of the year if every pair of rabbits give birth to a new pair every month, (but the newborn rabbit pair will start giving birth from the second month)?
The resulting number sequence is 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
If you ask what these numbers mean let us tell you, that it was noticed later that when these numbers are divided by each other the number 1,618033… is the result which is widely used in nature and many places in the universe.
But it would be wrong to say that it is used everywhere or continuously because it is just one of the ratios that we have discovered so far. There are writings about the human body describing that as the harmony of the combined particles come closer to the Golden Ratio they approach the average.
Places Where the Golden Ratio is Seen and Found
In Plants
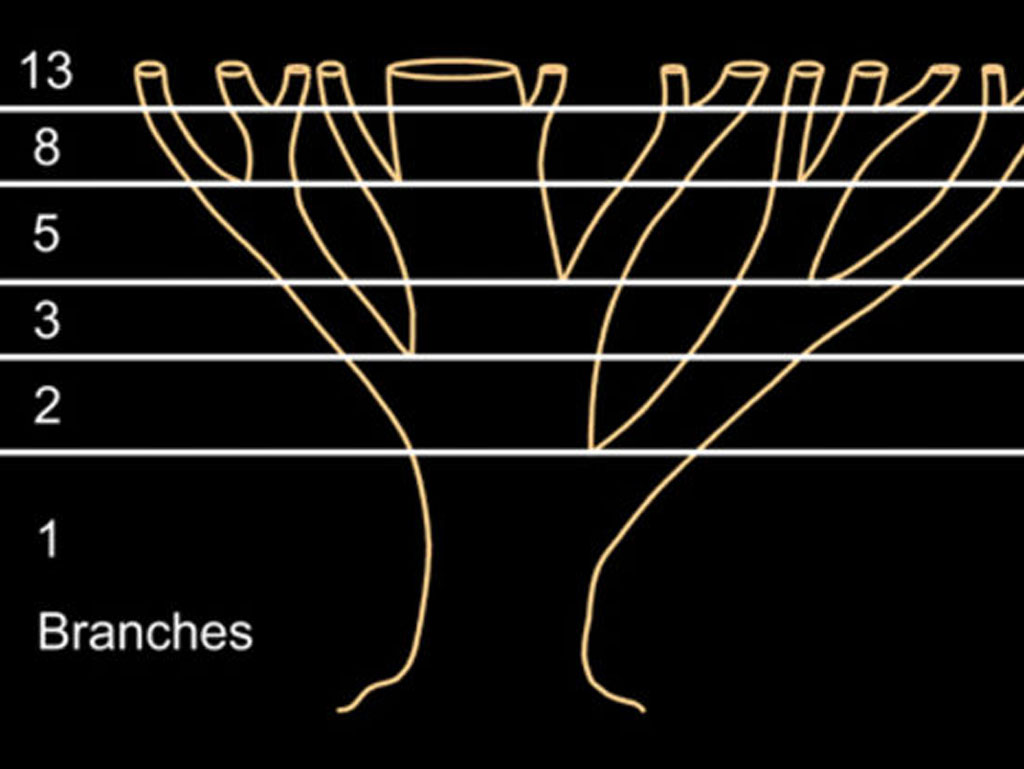
The most common examples are plants’ petals, sunflowers, cones, aloe plants and similar plants. As you can see below, some tree branches produce new branches similar to the Fibonacci number sequence.
In Humans
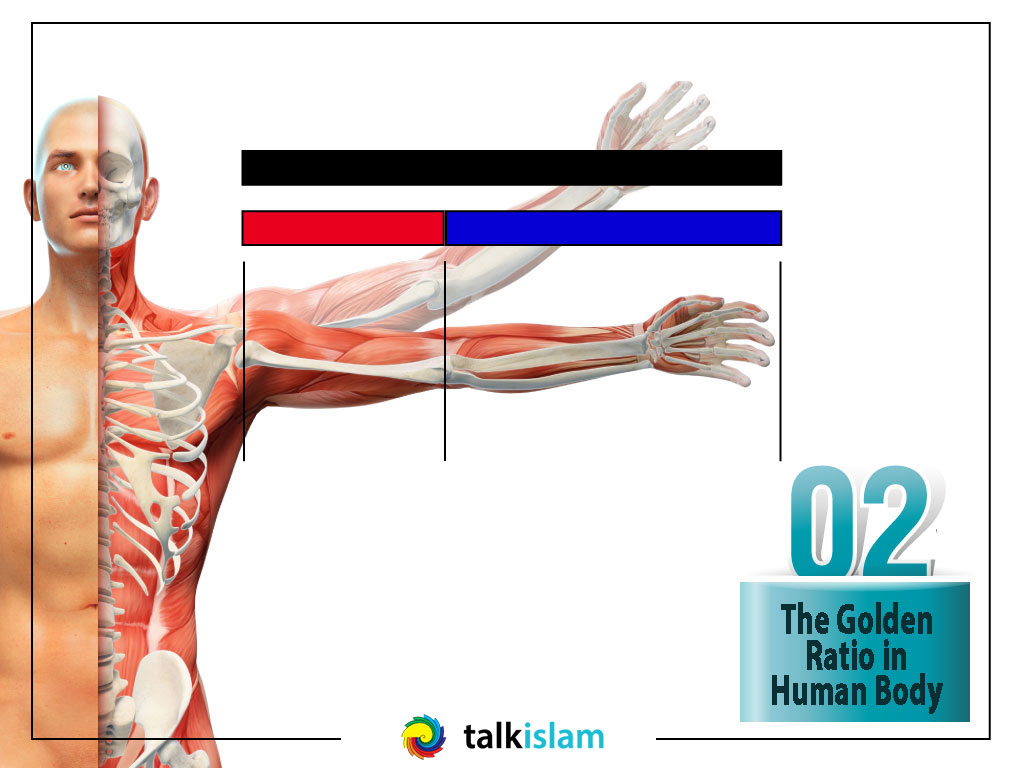
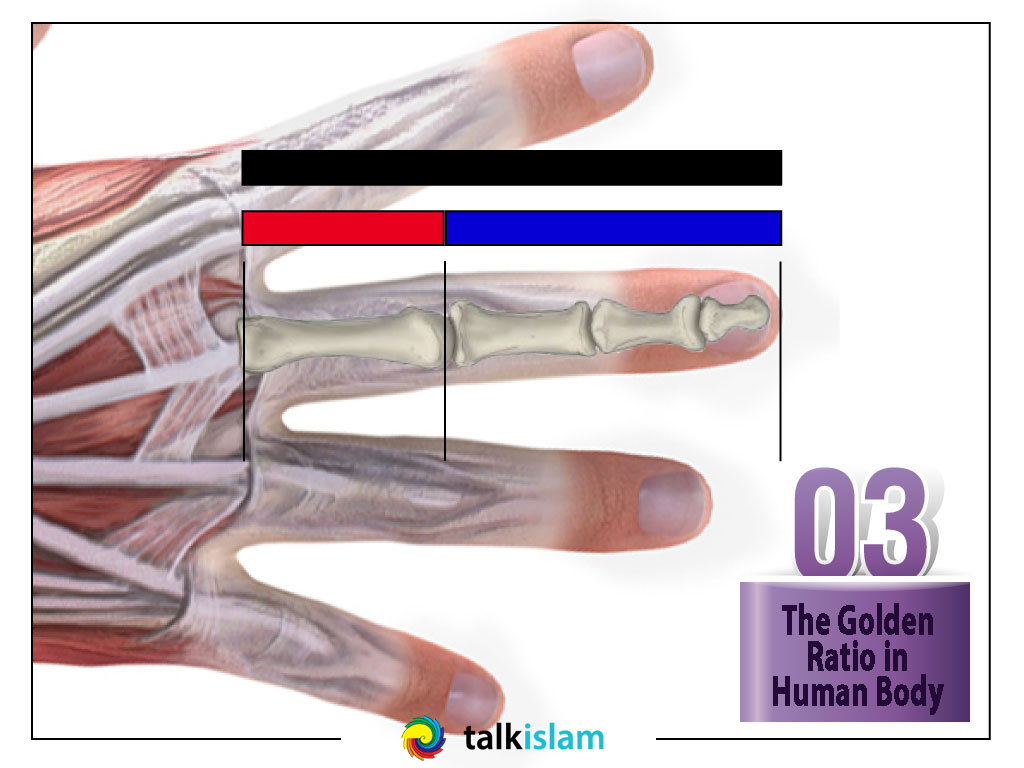
We come across the gold ratio many times on our bodies. For example, our belly-button is situated at a golden ratio in relation to our height. If we divide our arms from our elbows, we come across the golden ratio. The golden ratio can be found in the human fingers or the face.
It is important to note that the body of each individual shows different proportions, but if we look at the average in general we see that we are closer to the Golden Ratio.
In Animals
Nautilus shells living in the deep waters of the South Pacific are a perfect example of the Golden Ratio. In addition to this, there are examples of the golden ratio in starfish, dolphins, honey bees and ants.
In the Universe
The spiral arms of the Milky Way Galaxy, where our solar system is located, are a good example of the Golden Ratio. We also come across this ratio in storms and whirlpools. Below you can see a satellite picture of Hurricane Sandy which hit the continent of America in 2012.
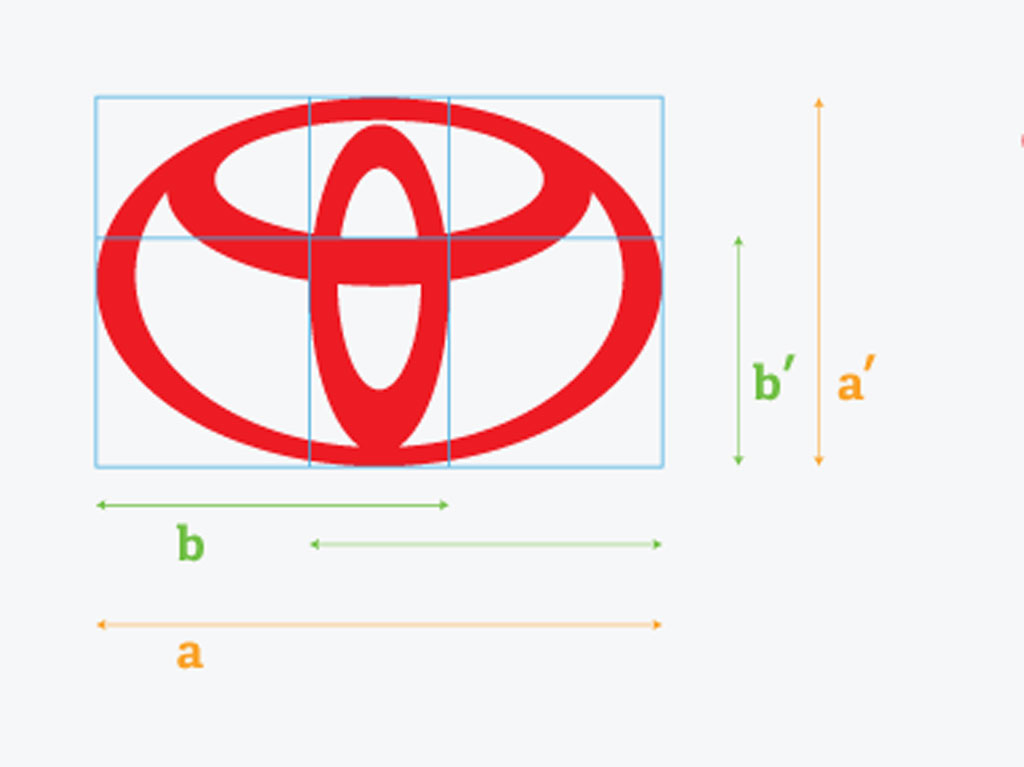
In Brands
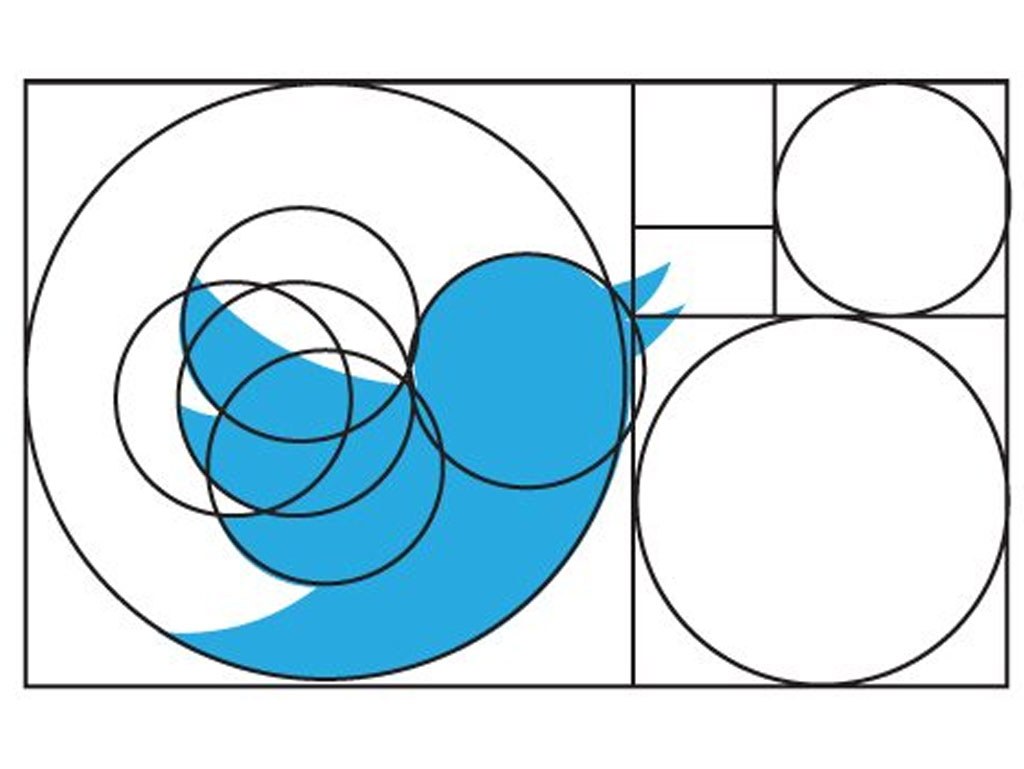
Brands such as Toyota, Mercedes, Twitter, Apple, Google, Pepsi have benefited from the ideal Golden Ratio when designing their logos.
Who is Leonardo Fibonacci?
Leonardo Pisano (Leonardo of Pisa) or widely known as Fibonacci is one of the most talented mathematicians of the Middle Ages. It is thought that he was born in Pisa in 1170.
Childhood
Fibonacci’s journey in algebra begins with the appointment of his father, a Pisalian merchant named Guglielmo, as a consul to the North African port of Bugia (now Bejaya, Algeria).
His father hired an Arab teacher to teach Fibonacci to make calculations, and then Fibonacci realized that making calculations with Indian-Arab numbers was much simpler than Roman figures.
Fibonacci will later describe these figures as follows: “Nine Indian figures are 9 8 7 6 5 4 3 2 1. By adding the number “0” to these digits, any number can be written down.
Leonardo had the opportunity to work with the leading Arabian mathematicians of the time by visiting the Mediterranean region until 1200.
His Works
Liber Abaci
When Fibonacci published this work, no one except a few “intellectuals” knew about the Hindu-Arab numbers. Liber Abaci drew great attention after he was published, his work was printed many times, and the Arab numbers began to spread among the Italian merchants (despite the prohibition of the church).
In the meantime, the book drew the attention of the Roman Emperor Frderick II. who was fond of science. The Emperor calls Fibonacci in 1220 and makes him take an exam and when he sees that he is very successful he keeps him near him.
Liber Quadratorum
Fibonacci dedicate his book Liber Quadratorum (The Book of Squares), which he wrote in 1225 to the emperor. The book, which was not as popular as Liber Abaci became in fact a masterpiece and had greatly contributed to the theories of numbers.
The Rabbit Problem and the Golden Ratio
Leonardo Fibonacci is named as “The person who takes Mathematics from the Arabs and transfers it to Europe” but his name is now known for a number sequence that arises in a problem in Liber Abaci that I will talk about a little later.
The problem which is about the Fibonacci Numbers 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…. is as follows:
Put a pair of rabbits in a room with all sides surrounded by walls. How many pairs of rabbits are there at the end of the year if every pair of rabbits give birth to a new pair every month, (but the newborn rabbit pair will start giving birth from the second month)?
In fact, according to our estimations, the answer to this question, is an addition exercise, which the answer is found by adding the previous answer and finding a new result, and the number 1,618033…. is found when these numbers are divided by each other. This number has become very popular when it was realized that it was used in many places in nature and the universe.













Get Social